Một trong những loại hình không gian quen thuộc bên cạnh hình cầu, hình chóp, lăng trụ,… thì không thể không kể đến hình trụ. Vì thế, bài viết dưới đây chúng tôi sẽ chia sẻ công thức tính thể tích hình trụ hình nón. Từ đó, giúp bạn có thể vận dụng công thức tính thể tích hình trụ linh hoạt để áp dụng vào giải các bài toán hình học không gian cho đơn giản nhất nhé!
| ➥ Xem thêm: |
Nội dung bài viết
I. Hình trụ là gì?
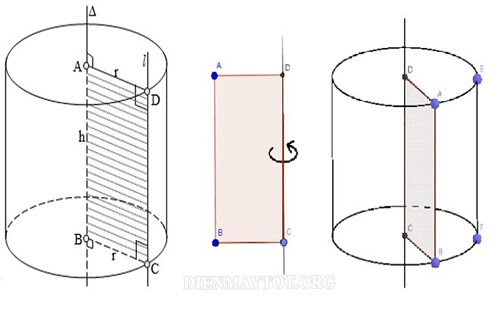
Hình trụ là hình có 2 mặt đáy là 2 hình tròn song song với nhau và bằng nhau. Trong cuộc sống các bạn có thể dễ dàng gặp phải các đồ vật có hình trụ như cái cốc, lon sữa bò, lọ hoa, cái xô, cái thùng,…
Tham khảo:
- ▷Cách tính múi giờ Trái Đất &10 “BÍ MẬT THÚ VỊ”
II. Tính bán kính, chiều cao và diện tích hình trụ
Tìm bán kính đáy hình trụ
Đáy hình trụ bằng nhau nên ta chỉ cần tìm một mặt. Thường thì bán kính đáy được cho trong giả thiết nên không cần tìm. Hoặc giả thiết cho đường kích thì chúng ta chỉ việc lấy đường kích chia đôi là ra bán kính. r=d/2
Tính chiều cao của hình trụ
Bạn cũng có thể lấy thước đo hoặc đây là thông tin được cho trong giả thiết để cung cấp và tính được thể tích hình trụ. Chiều cao chính là khoảng cách giữa đáy trên và đáy dưới.
Công thức tính diện tích hình trụ
Diện tích toàn phần của hình trụ tròn bằng diện tích xung quanh cộng diện tích 2 đáy. Trong đó, diện tích xung quanh bằng chu vi đường tròn đáy nhân chiều cao.
Ta có công thức tính diện tích hình trụ tròn như sau:
Sxq = 2.r.h
Stp = Sxq + S2 đáy = 2.r.h + 2r² = 2.r.(r + h)
Trong đó:
- Sxq: là diện tích xung quanh hình trụ
- Stp: Diện tích toàn phần của hình trụ tròn
- r: Bán kính hình tròn mặt đáy hình trụ
- π là hằng số pi = 3.14
- h: chiều cao của hình trụ
III. Công thức tính thể tích hình trụ tròn
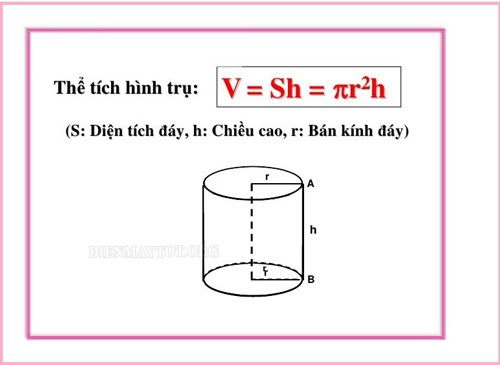
Công thức tính thể tích hình trụ rỗng như sau:
V= π. r². h
Trong đó công thức tính thể tích khối trụ có như sau:
- V là thể tích của hình trụ (m³)
- r: Bán kính hình tròn mặt đáy hình trụ
- π là hằng số pi = 3.14
- h: chiều cao của hình trụ
IV. Bài tập minh hoạ cách tính thể tích hình trụ
1. Dạng bài tính thể tích khi biết chiều cao và bán kính đáy
Câu hỏi: Cho khối trụ (H) có đáy là hình tròn ngoại tiếp tam giác đều có cạnh là a, và chiều cao của khối trụ bằng 4a. Hãy tính thể tích V của khối trụ (H).
Lời giải:
- Bán kính đáy của khối trụ là r = (a√3)/3
- Từ đó, ta có thể tích khối trụ là V = π. r².h = π.((a√3)/3)².4a=(4/3).π.a³
>> Tham khảo thêm: ▶Công thức diện tích mặt cầu ▶thể tích khối cầu【KÈM VÍ DỤ】
2. Dạng bài tính bán kính đáy khi biết chiều cao và thể tích
Câu hỏi: Cho khối trụ có thể tích bằng π.a3 và có chiều cao là 3a. Hãy tính bán kính đáy r của khối trụ đó.
Lời giải:
Áp dụng công thức: V = π. r². h
=> r² = V/(π.h)= (π.a³)/π.3a= a²/3=> r= a/√3
3. Dạng bài tính chiều cao khi biết bán kính đáy và thể tích
Câu hỏi: Cho hình trụ có chu vi đáy C = 4π và thể tích của khối trụ là V=12π. Hãy tính chiều cao của khối trụ đã cho.
Lời giải:
Theo bài ra ta có, bán kính đáy của khối trụ là: r = C/2π= 2
Từ đó, ta có chiều cao hình trụ là h = V/π.r²= 12π/π.4= 3
>> Tham khảo thêm: Các công thức lượng giác lớp 10 CẦN NHỚ “Cơ bản – Nâng cao”
4. Dạng bài tập dây cung hình trụ
Đây là dạng bài nâng cao hơn, nó liên quan tới đoạn thẳng nối 2 điểm nằm lần lượt trên 2 đường tròn đáy của hình trụ. Lưu ý, đây không phải là dây cung của đường tròn đáy.
Nếu dây cung không trùng với đường sinh thì dây cung sẽ nằm ở trong hình trụ và ngược lại, nếu dây cung trùng với đường sinh thì sẽ nằm trên mặt xung quanh của hình trụ.
Câu hỏi: Cho hình trụ H có 2 đáy là 2 đường tròn tâm O và O’. Điểm A và điểm B nằm lần lượt trên đường tròn O và O’, biết rằng AB có độ dài bằng a và AB tạo với trục OO’ một góc , khoáng cách giữa OO’ với AB bằng d. Hãy tính thể tích khối trụ H theo a và.
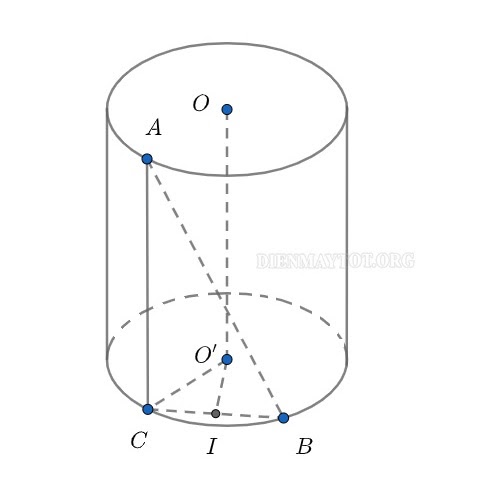
Lời giải:
Gọi điểm C là hình chiếu của A trên đường tròn O’ và I là trung điểm của BC. Lúc này ta có góc BAC là góc giữa trục OO’ và dây AB, hay góc BAC = α
Chiều cao của khối trụ đã cho là h = OO’ = AB. cos α= a cos α
Tương tự ta cũng có BC = AB. sin α = asin α=> IC = ½ asin α
I là trung điểm của BC và O’I vuông góc với BC nên khoảng cách từ OO’ đến AB chính là O’I = d
Trong tam giác vuông O’IC ta có:
O’C² = IC² + O’I² = 14a²sin²α+ d² = r²
Thể tích của khối trụ H:
V = π. r². h = π. (1/4(a²sin²α+ d²).a cos α
Trên đây là một số thông tin chia sẻ về công thức tính thể tích hình trụ cũng như các dạng bài tập thường gặp. Hy vọng với những chia sẻ trên sẽ giúp các bạn có thêm thông tin và biết cách giải các dạng bài tập này. Chúc các bạn có buổi học vui vẻ và lý thú.
Xem thêm các công thức toán học khác:

![[Tổng hợp] Bảng công thức nguyên hàm từ “cơ bản – nâng cao” Bảng công thức nguyên hàm đầy đủ](https://dienmaytot.org/wp-content/uploads/2020/10/cong-thuc-nguyen-ham-co-ban.jpg)






