Trong toán học, mỗi loại hình sẽ có những đặc điểm nhận dạng và công thức tính toán khác nhau. Trong bài viết này chúng tôi sẽ cung cấp cho các bạn về khái niệm, công thức tính chu vi và công thức tính diện tích hình bình hành đơn giản và dễ hiểu nhất.
Nội dung bài viết
I. Dấu hiệu nhận biết hình bình hành
Hình bình hành là hình tứ giác có một cặp cạnh đối song song và bằng nhau hoặc 2 cặp cạnh đối song song với nhau.
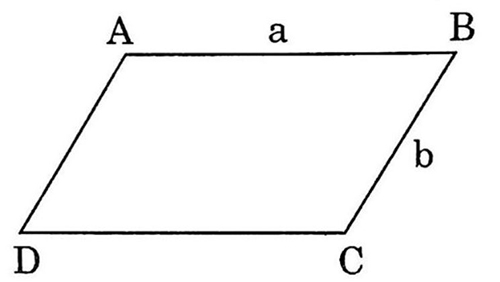
Tính chất của hình bình hành: Hình bình hành có 2 đường chéo cắt nhau tại trung điểm của mỗi đường và có 2 góc đối bằng nhau. Hình bình hành cũng là hình thang, nên nó có đầy đủ tính chất của hình thang.
II. Công thức tính chu vi hình bình hành
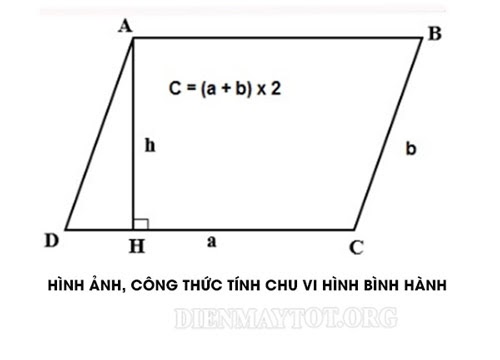
Chu vi của hình bình hành bằng 2 lần tổng của 1 cặp cạnh kề nhau bất kỳ. Hoặc có thể hiểu theo cách khác là tổng độ dài của 4 cạnh. Chu vi hình bình hành:
C = (a + b) x 2
Trong đó:
- C là chu vi của hình bình hành
- a và b là độ dài hai cạnh bất kỳ của hình bình hành
| ➥ Xem thêm: |
III. Công thức tính diện tích hình bình hành
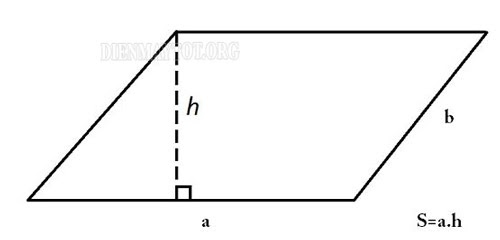
Diện tích hình bình hành bằng tích chiều cao nhân với cạnh đáy. Công thức như sau:
S = a x h
Trong đó:
- a là cạnh đáy của hình bình hành
- h là chiều cao nối từ đỉnh tới đáy của hình bình hành
Từ công thức tính diện tích thì chúng ta cũng có thể suy ra công thức tính chiều cao hình bình hành như sau:
h = S/a
| ➥ Xem thêm: |
IV. Dạng bài tập toán lớp 4 tính chu vi, diện tích hình bình hành
1. Dạng bài tính chu vi
Ví dụ minh hoạ: Cho hình bình hành ABCD có 2 cạnh a và b lần lượt là 10cm và 15cm. Vậy chu vi của hình bình hành ABCD là bao nhiêu?
Lời giải:
Áp dụng công thức chu vi hình bình hành ta có:
C = (a + b) x 2 = (10 + 15) x 2 = 50cm.
2. Dạng bài tính diện tích
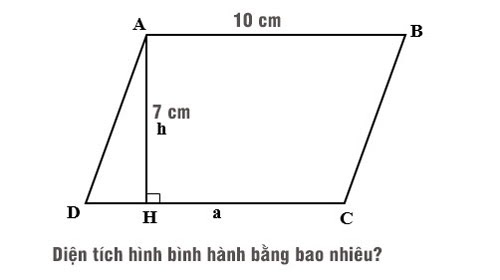
Ví dụ minh họa: Cho hình bình hành ABCD có chiều dài của cạnh đáy CD = 10cm và chiều cao nối từ đỉnh A xuống cạnh CD bằng 7cm. Vậy hình bình hành ABCD có diện tích là bao nhiêu?
Lời giải:
Áp dụng công thức diện tích hình bình hành:
SABCD = a x h = 10 x 7 = 70cm²
3. Dạng bài tìm độ dài đáy
Ví dụ: Hãy tìm độ dài đáy của hình bình hành ABCD có diện tích 45cm2 và chiều cao AH là 10cm.
Lời giải: Độ dài đáy của hình bình hành là AB = CD = SABCD /h = 45/10 = 4.5cm
4. Dạng bài tìm chiều cao
Ví dụ: Hãy tính chiều cao AH của hình bình hành ABCD khi biết diện tích là 50cm2 và độ dài cạnh đáy AB là 20cm.
Lời giải: Chiều cao của hình bình hành là: AH = SABCD / AB = 50/20= 2.5cm
5. Bài tập dạng nâng cao
Ví dụ: Cho hình bình hành ABCD có cạnh đáy AB là 50cm. Sau đó, người ta thu hẹp hình bình hành này bằng cách giảm các cạnh đáy của hình bình hành đi 15cm thì thu được hình bình hành mới AEID có diện tích nhỏ hơn diện tích hình bình hành ban đầu là 90cm2. Hãy tính diện tích hình bình hành ABCD ban đầu
Lời giải:
h: Chiều cao của hình bình hành ABCD
Ta có diện tích của hình bình hành ABCD là:
SABCD = 50xh
Diện tích của hình bình hành AEID sau khi giảm đi cạnh đáy 15cm là:
SAEID = AE x h = (50 – 15) x h= 35 x h
Mà SABCD = SAEID + 90
=> 50 x h = 35 x h + 90
=> 15h = 90 => h = 90/15 = 6cm.
Vậy diện tích của hình bình hành ABCD ban đầu là:
SABCD = 50 x h = 50 x 6 = 300 cm²
Bài viết trên đây chúng tôi đã chia sẻ với các bạn về công thức tính chu vi và công thức tính diện tích hình bình hành và 1 vài dạng bài toán từ cơ bản đến nâng cao. Riêng đối với các bài tập dạng nâng cao các bạn cần vận dụng các kiến thức đã học kết hợp với mối liên giữa các công thức tính chu vi, diện tích để tìm được bài giải chính xác nhất cho bài toán của mình.
>>> Theo dõi thêm tại website: https://dienmaytot.org/
Xem thêm các công thức toán học hay khác:
